Post

Understanding The Intuitive Idea of Attention

Posted Updated
By Ahammad Nafiz 24 min read

Intro

Table of Contents

  1. The Information Bottleneck in Vanilla Seq2Seq
  2. The Intuitive Idea of Attention
  3. Mathematical Formulation of Attention
  4. Deep Dive: Step-by-Step Mathematical Derivations
  5. Detailed Example: Bengali→English Translation
  6. Bahdanau vs. Luong Attention: Architectural Deep Dive
  7. Mathematical Properties and Theoretical Analysis
  8. Information-Theoretic Perspective
  9. Gradient Flow and Training Dynamics
  10. Real-World Applications
  11. Quick Revision Summary
  12. References

The Information Bottleneck in Vanilla Seq2Seq

The information bottleneck problem in traditional seq2seq models showing how all source sequence information must be compressed into a single fixed-size vector, creating a severe bottleneck that leads to information loss especially for longer sequences

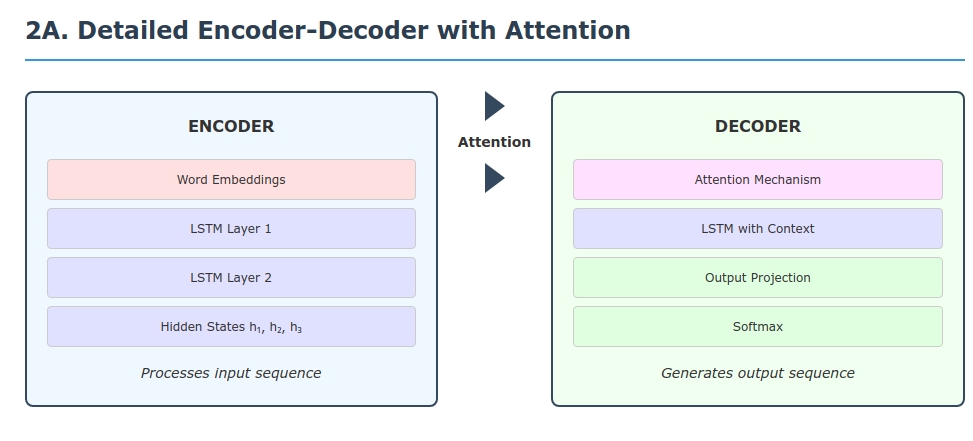
In a basic encoder–decoder (seq2seq) model, the encoder compresses an entire input sequence $x_1,\dots,x_T$ into a single fixed-size vector (often the last hidden state $h_{\text{final}}$). The decoder then generates all outputs $y_1,\dots,y_S$ from this one vector. Formally:

Encoder: $x_1,\dots,x_T \;\longrightarrow\; h_{\text{final}}$. Decoder: $h_{\text{final}} \;\longrightarrow\; y_1,\dots,y_S$.

This creates a severe information bottleneck. All information about a sentence of length $T$ must be squashed into one vector. As Bahdanau et al. explain, a fixed-length context tends to forget early words and degrades for long sentences. In practice, translation accuracy drops sharply as sentence length grows. Moreover, the decoder sees a static context: it uses the same $h_{\text{final}}$ to predict every output word. Intuitively, this is like trying to translate by looking at a blurry snapshot of the entire source sentence – you cannot dynamically focus on particular words. Attention mechanisms were introduced precisely to break this bottleneck, as described next.

The Intuitive Idea of Attention

Visual representation of the attention mechanism concept showing how it allows the model to dynamically focus on different parts of the input sequence when generating each output token, similar to a movable spotlight

Instead of a fixed summary, attention lets the model focus on different parts of the input when generating each output. In human terms, when translating we often concentrate on one phrase at a time. For example, translating “আমি বাংলাদেশে বাস করি” → “I live in Bangladesh”: a human translator might first focus on “আমি” and say “I”, then focus on “বাস করি” to say “live”, and finally on “বাংলাদেশে” for “in Bangladesh”.

Attention is like a movable spotlight over the input sequence: for each output position $i$, the model assigns a weight $\alpha_{ij}$ (the “brightness” on word $j$) and draws a context vector as a weighted summary of the input. As Xu et al. demonstrate in image captioning, an attention-based model can automatically “fix its gaze” on salient objects (here, words or image regions) when generating each word. Concretely, the attention weights form a probability distribution over source positions (summing to 1), so the decoder can softly attend to the most relevant words. This “soft alignment” is learned end-to-end.

Mathematical Formulation of Attention

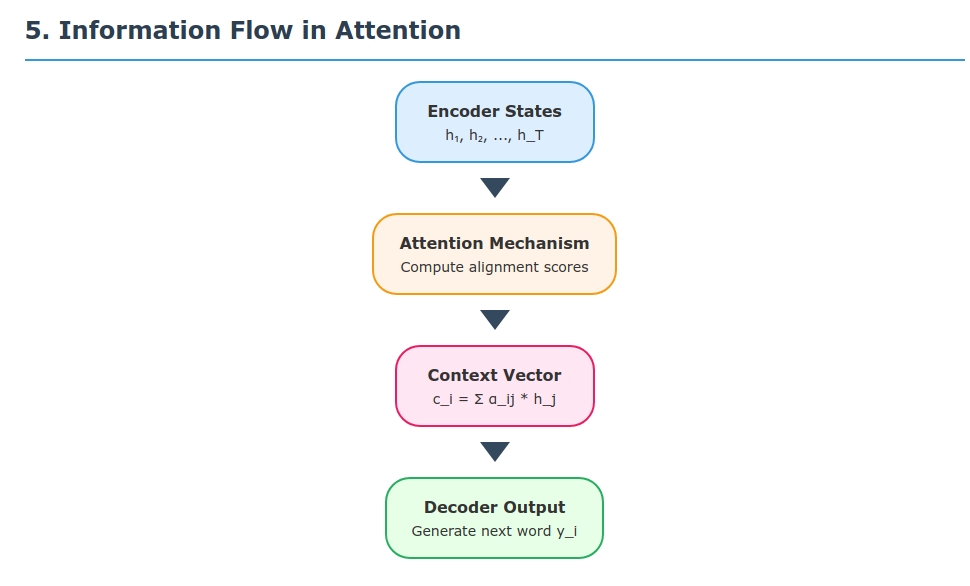
Attention introduces a few new quantities alongside the usual seq2seq variables. Suppose the encoder produces hidden states

Detailed architecture diagram of an encoder-decoder model with attention mechanism, showing the flow of information from input tokens through encoder hidden states to attention-weighted context vectors for decoder processing

\[h_1, h_2, \dots, h_T \in \mathbb{R}^d\]

for each of the $T$ input tokens. The decoder has hidden states

\[s_1, s_2, \dots, s_S \in \mathbb{R}^d\]

for each of the $S$ output tokens. Attention defines a context vector $c_i$ for each decoder step $i$ as a weighted sum of the encoder states:

\[c_i = \sum_{j=1}^T \alpha_{ij}\, h_j\,.\]

Here, $\alpha_{ij}$ is the attention weight on source position $j$ when predicting output $i$. These weights are computed by first scoring each encoder state against the current decoder state, then normalizing:

Step-by-step visualization of attention computation showing the process from encoder hidden states through alignment scoring to normalized attention weights and context vector construction

  1. Alignment scores: Compute raw scores $e_{ij}$ measuring compatibility between decoder state and encoder state. There are two main styles:

    • Bahdanau (additive) attention (2014): uses the previous decoder state $s_{i-1}$. For example, Bahdanau et al. use a small neural net:

      \[e_{ij} = \mathbf{v}_a^\top \tanh(\mathbf{W}_a[s_{i-1}; h_j] + b_a),\]

      where $[s_{i-1}; h_j]$ is the concatenation of states.

    • Luong (multiplicative) attention (2015): typically uses the current decoder state $s_i$. A simple version is the dot-product:

      \[e_{ij} = s_i^\top h_j,\]

      or more generally $s_i^\top \mathbf{W}_a h_j$.

  2. Attention weights (softmax): Convert scores to probabilities via softmax:

    \[\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^T \exp(e_{ik})}\,.\]

    By construction, each $\alpha_{ij}\ge0$ and $\sum_{j}\alpha_{ij}=1$. Intuitively, $\alpha_{ij}$ is the (soft) alignment between target position $i$ and source position $j$.

  3. Context vector: Form the context $c_i$ as above. This vector is essentially a weighted average of encoder states – the expected value of the input states under the attention distribution. It captures the relevant information needed to produce $y_i$.

  4. Decoder update: The decoder then uses $c_i$ along with its previous state/output to generate the next word. In Bahdanau’s formulation, the context $c_i$ is fed into the RNN update:

    \[s_i = \text{LSTM}(s_{i-1}, y_{i-1}, c_i),\]

    and then $y_i$ is predicted from $s_i$ (and possibly $c_i$). In Luong’s formulation, one first updates $s_i=\text{LSTM}(s_{i-1},y_{i-1})$ without context, and then computes $c_i$ using $s_i$, combining them afterward.

This mechanism is entirely differentiable, so the alignment function $f_{\text{att}}$ (the weights $\mathbf{v}_a, \mathbf{W}_a$, etc.) is learned jointly with the rest of the model. In summary:

  • Context: $c_i = \sum_{j=1}^T \alpha_{ij}\,h_j$.
  • Scores: $e_{ij} = f_{\text{att}}(s_{i-1},h_j)$ or $f_{\text{att}}(s_i,h_j)$.
  • Weights: $\alpha_{ij} = \text{softmax}(e_{ij})$.

These formulas and distributions are described in detail in the NMT literature.

Deep Dive: Step-by-Step Mathematical Derivations

Mathematical formulation diagram showing the core attention mechanism equations including alignment scores, softmax normalization, and context vector computation with detailed mathematical notation

Why Softmax? The Probability Distribution Intuition

Question: Why do we use softmax normalization for attention weights? Why not just use the raw scores $e_{ij}$?

Answer: The softmax function serves multiple crucial purposes:

  1. Normalization Constraint: We want $\sum_{j=1}^T \alpha_{ij} = 1$ so that the context vector $c_i$ is a proper weighted average. Without normalization, some positions might receive arbitrarily large weights.

  2. Non-negativity: Softmax ensures $\alpha_{ij} \geq 0$, making the weights interpretable as “attention strengths.”

  3. Differentiability: The softmax function is smooth everywhere, enabling gradient-based learning.

  4. Competition: Softmax creates competition between positions—if one score increases, others effectively decrease in relative importance.

Mathematical Derivation:

Starting with raw scores $e_{i1}, e_{i2}, \ldots, e_{iT}$, we want to transform them into a probability distribution. The softmax function is:

\[\alpha_{ij} = \frac{\exp(e_{ij})}{\sum_{k=1}^T \exp(e_{ik})}\]

Why exponential? The exponential function has several desirable properties:

  • Always positive: $\exp(x) > 0$ for all $x$
  • Monotonic: if $e_{ij} > e_{ik}$, then $\exp(e_{ij}) > \exp(e_{ik})$
  • Amplifies differences: large differences in scores become even larger after exponentiation

Verification of probability properties: \(\sum_{j=1}^T \alpha_{ij} = \sum_{j=1}^T \frac{\exp(e_{ij})}{\sum_{k=1}^T \exp(e_{ik})} = \frac{\sum_{j=1}^T \exp(e_{ij})}{\sum_{k=1}^T \exp(e_{ik})} = 1\)

Temperature parameter: Sometimes we use a temperature $\tau$: \(\alpha_{ij} = \frac{\exp(e_{ij}/\tau)}{\sum_{k=1}^T \exp(e_{ik}/\tau)}\)

  • $\tau > 1$: “softer” attention (more uniform distribution)
  • $\tau < 1$: “sharper” attention (more peaked distribution)
  • $\tau \to 0$: approaches hard attention (one-hot distribution)

The Attention Score Function: Design Choices

Comparative diagram illustrating the key differences between Bahdanau attention (additive/concat) and Luong attention (multiplicative/dot-product) showing their respective architectures and computational approaches

Question: How do we design the function $f_{\text{att}}(s, h)$ that computes compatibility between decoder and encoder states?

Bahdanau (Additive) Attention: \(e_{ij} = \mathbf{v}_a^T \tanh(\mathbf{W}_a [s_{i-1}; h_j] + \mathbf{b}_a)\)

Step-by-step breakdown:

  1. Concatenation: $[s_{i-1}; h_j] \in \mathbb{R}^{2d}$ combines decoder and encoder information
  2. Linear transformation: \(\mathbf{W}_a [\mathbf{s}_{i-1}; \mathbf{h}_j] + \mathbf{b}_a\) projects to hidden space
    • $\mathbf{W}_a \in \mathbb{R}^{d_a \times 2d}$ (learnable weight matrix)
    • $\mathbf{b}_a \in \mathbb{R}^{d_a}$ (learnable bias vector)
    • $d_a$ is the attention hidden dimension
  3. Non-linearity: $\tanh(\cdot)$ introduces non-linear interactions
  4. Projection to scalar: $\mathbf{v}_a^T$ projects the $d_a$-dimensional vector to a scalar score

Why this architecture?

  • Flexibility: The MLP can learn complex relationships between $s$ and $h$
  • Symmetry breaking: Without the MLP, the model might not learn meaningful alignments
  • Expressiveness: Can model non-linear compatibility functions

Luong (Multiplicative) Attention:

Three variants are proposed:

  1. Dot product: $e_{ij} = s_i^T h_j$
  2. General: $e_{ij} = s_i^T \mathbf{W}_a h_j$
  3. Concat: $e_{ij} = \mathbf{v}_a^T \tanh(\mathbf{W}_a [s_i; h_j])$

Dot product derivation: \(e_{ij} = s_i^T h_j = \sum_{k=1}^d s_i^{(k)} h_j^{(k)}\)

This measures the cosine similarity (when normalized) between the decoder and encoder states. High similarity → high attention weight.

When does dot product work well?

  • When encoder and decoder states live in the same semantic space
  • When the hidden dimensions are the same ($s_i, h_j \in \mathbb{R}^d$)
  • Computationally efficient: $O(d)$ operations vs. $O(d^2)$ for additive

General attention derivation: \(e_{ij} = s_i^T \mathbf{W}_a h_j = \sum_{k=1}^d \sum_{l=1}^d s_i^{(k)} W_a^{(k,l)} h_j^{(l)}\)

This learns a bilinear form that can transform the encoder space to match the decoder space.

Context Vector: Weighted Information Aggregation

Question: Why is the context vector defined as $c_i = \sum_{j=1}^T \alpha_{ij} h_j$? What does this achieve?

Intuitive explanation: The context vector is the expected value of encoder hidden states under the attention distribution:

\[c_i = \mathbb{E}_{j \sim P_i}[h_j] = \sum_{j=1}^T P_i(j) \cdot h_j = \sum_{j=1}^T \alpha_{ij} h_j\]

where $P_i(j) = \alpha_{ij}$ is the probability of attending to position $j$ at decoder step $i$.

Mathematical properties:

  1. Convex combination: Since $\alpha_{ij} \geq 0$ and $\sum_j \alpha_{ij} = 1$, the context vector $c_i$ lies in the convex hull of ${h_1, h_2, \ldots, h_T}$.

  2. Information preservation: If attention is uniform ($\alpha_{ij} = 1/T$), then $c_i$ is the average of all encoder states. If attention is peaked ($\alpha_{ij} \approx 1$ for some $j$), then $c_i \approx h_j$.

  3. Dimensionality: $c_i \in \mathbb{R}^d$ has the same dimension as encoder states, making it easy to integrate into the decoder.

Alternative aggregation methods:

  • Max pooling: $c_i = \max_j(\alpha_{ij} \odot h_j)$ (element-wise)
  • Concatenation: $c_i = [\alpha_{i1} h_1; \alpha_{i2} h_2; \ldots; \alpha_{iT} h_T]$ (much higher dimensional)
  • Attention-weighted norm: $c_i = \sum_j \alpha_{ij} |h_j|$

The weighted sum is chosen because it preserves semantic information while being computationally tractable.

Detailed Example: Bengali→English Translation

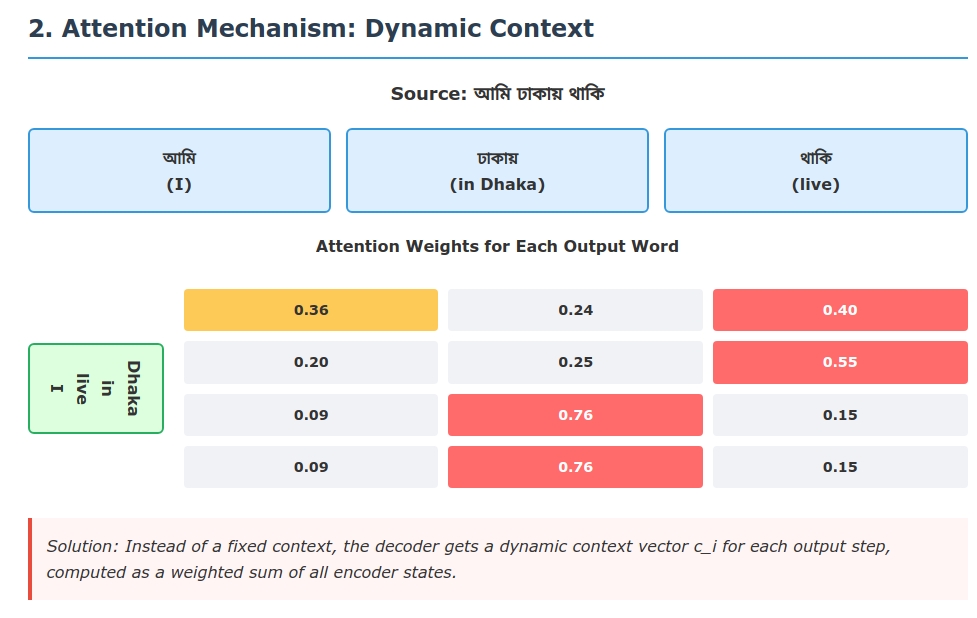
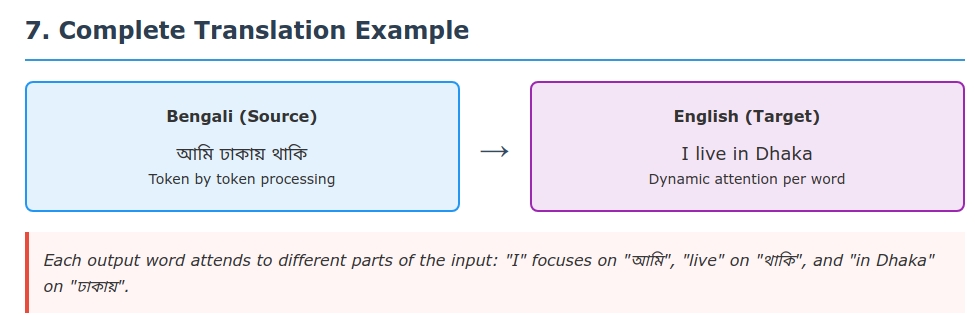
Let’s walk through a comprehensive example to see attention in action with complete mathematical details. We’ll translate “আমি ঢাকায় থাকি” (“I live in Dhaka”) step by step.

Information flow diagram in attention mechanism showing how encoder hidden states are processed through attention weights to create dynamic context vectors that flow to the decoder at each time step

Setup and Initialization

Input processing:

  • Tokenization: [“আমি”, “ঢাকায়”, “থাকি”] → [1, 2, 3] (token IDs)
  • Embedding: Each token → 4-dimensional vector (for simplicity)
  • Encoder: Bidirectional LSTM produces hidden states

Encoder hidden states (artificially constructed for demonstration):

  • $\mathbf{h}_1 = [0.2, -0.1, 0.8, 0.3]$ (for “আমি” = I)
  • $\mathbf{h}_2 = [0.5, 0.7, -0.2, 0.6]$ (for “ঢাকায়” = in Dhaka)
  • $\mathbf{h}_3 = [-0.3, 0.4, 0.9, -0.1]$ (for “থাকি” = live)

Decoder initialization:

  • $\mathbf{s}_0 = [0.1, 0.0, -0.2, 0.1]$ (initial decoder state)
  • Start token: <START> → embedding $\mathbf{e}_{\text{start}} = [0.0, 0.1, 0.0, 0.0]$

Step 1: Generate “I” (Detailed Calculation)

1.1 Compute attention scores (using Bahdanau attention):

For Bahdanau attention, we need:

  • $\mathbf{W}_a \in \mathbb{R}^{2 \times 8}$ (transforms 8D concatenated vector to 2D)
  • $\mathbf{v}_a \in \mathbb{R}^{2}$ (projects to scalar)
  • $\mathbf{b}_a \in \mathbb{R}^{2}$ (bias term)

Let’s use these parameter values: \(\mathbf{W}_a = \begin{bmatrix} 0.5 & -0.2 & 0.1 & 0.3 & 0.7 & 0.0 & -0.1 & 0.4 \\ 0.2 & 0.6 & -0.3 & 0.1 & 0.0 & 0.8 & 0.2 & -0.2 \end{bmatrix}\)

\[\mathbf{v}_a = \begin{bmatrix} 0.8 \\ -0.3 \end{bmatrix}, \quad \mathbf{b}_a = \begin{bmatrix} 0.1 \\ -0.1 \end{bmatrix}\]

Score computation for $e_{1,1}$ (attending to “আমি”):

  1. Concatenate: $[\mathbf{s}_0; \mathbf{h}_1] = [0.1, 0.0, -0.2, 0.1, 0.2, -0.1, 0.8, 0.3]$

  2. Linear transformation: \(\mathbf{W}_a [\mathbf{s}_0; \mathbf{h}_1] = \begin{bmatrix} 0.5 & -0.2 & 0.1 & 0.3 & 0.7 & 0.0 & -0.1 & 0.4 \\ 0.2 & 0.6 & -0.3 & 0.1 & 0.0 & 0.8 & 0.2 & -0.2 \end{bmatrix} \begin{bmatrix} 0.1 \\ 0.0 \\ -0.2 \\ 0.1 \\ 0.2 \\ -0.1 \\ 0.8 \\ 0.3 \end{bmatrix}\)

    \[= \begin{bmatrix} 0.05 + 0 - 0.02 + 0.03 + 0.14 + 0 - 0.08 + 0.12 \\ 0.02 + 0 + 0.06 + 0.01 + 0 - 0.08 + 0.16 - 0.06 \end{bmatrix} = \begin{bmatrix} 0.24 \\ 0.11 \end{bmatrix}\]

  3. Add bias: \(\mathbf{W}_a [\mathbf{s}_0; \mathbf{h}_1] + \mathbf{b}_a = \begin{bmatrix} 0.24 \\ 0.11 \end{bmatrix} + \begin{bmatrix} 0.1 \\ -0.1 \end{bmatrix} = \begin{bmatrix} 0.34 \\ 0.01 \end{bmatrix}\)

  4. Apply tanh: \(\tanh\left(\begin{bmatrix} 0.34 \\ 0.01 \end{bmatrix}\right) = \begin{bmatrix} 0.327 \\ 0.010 \end{bmatrix}\)

  5. Project to scalar: \(e_{1,1} = \mathbf{v}_a^T \tanh(\cdot) = [0.8, -0.3] \begin{bmatrix} 0.327 \\ 0.010 \end{bmatrix} = 0.8 \times 0.327 - 0.3 \times 0.010 = 0.259\)

Similarly for other positions:

  • $e_{1,2} = -0.142$ (attending to “ঢাকায়”)
  • $e_{1,3} = 0.387$ (attending to “থাকি”)

Complete translation example demonstrating attention mechanism in action with Bengali to English translation, showing attention weights and alignment between source and target words throughout the translation process

1.2 Apply softmax normalization:

\[\alpha_{1,1} = \frac{\exp(0.259)}{\exp(0.259) + \exp(-0.142) + \exp(0.387)} = \frac{1.296}{1.296 + 0.868 + 1.472} = \frac{1.296}{3.636} = 0.357\] \[\alpha_{1,2} = \frac{\exp(-0.142)}{3.636} = \frac{0.868}{3.636} = 0.239\] \[\alpha_{1,3} = \frac{\exp(0.387)}{3.636} = \frac{1.472}{3.636} = 0.405\]

Verification: $0.357 + 0.239 + 0.405 = 1.001 \approx 1$ ✓

1.3 Compute context vector:

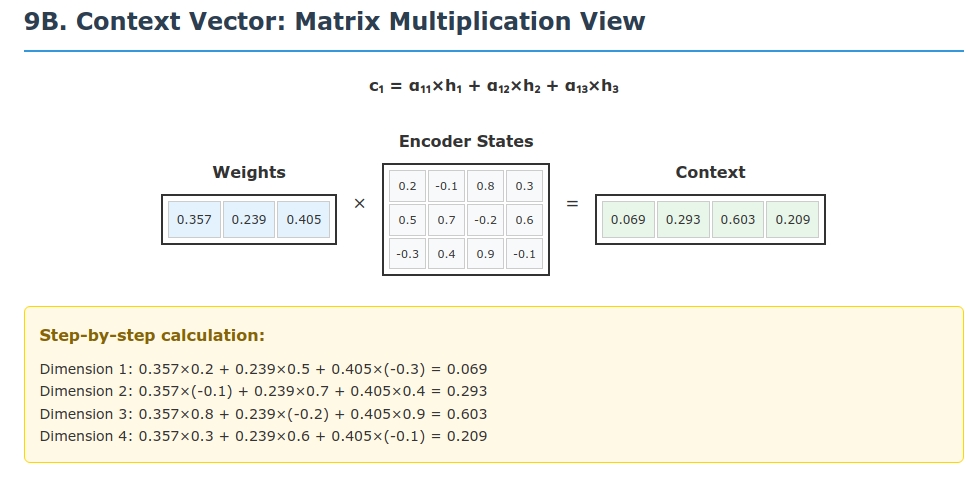
\[\mathbf{c}_1 = \alpha_{1,1} \mathbf{h}_1 + \alpha_{1,2} \mathbf{h}_2 + \alpha_{1,3} \mathbf{h}_3\] \[= 0.357 \begin{bmatrix} 0.2 \\ -0.1 \\ 0.8 \\ 0.3 \end{bmatrix} + 0.239 \begin{bmatrix} 0.5 \\ 0.7 \\ -0.2 \\ 0.6 \end{bmatrix} + 0.405 \begin{bmatrix} -0.3 \\ 0.4 \\ 0.9 \\ -0.1 \end{bmatrix}\] \[= \begin{bmatrix} 0.071 \\ -0.036 \\ 0.286 \\ 0.107 \end{bmatrix} + \begin{bmatrix} 0.120 \\ 0.167 \\ -0.048 \\ 0.143 \end{bmatrix} + \begin{bmatrix} -0.122 \\ 0.162 \\ 0.365 \\ -0.041 \end{bmatrix}\] \[= \begin{bmatrix} 0.069 \\ 0.293 \\ 0.603 \\ 0.209 \end{bmatrix}\]

1.4 Decoder update and word prediction:

In Bahdanau attention, the context vector is fed into the LSTM: \(\mathbf{s}_1 = \text{LSTM}(\mathbf{s}_0, \mathbf{e}_{\text{start}}, \mathbf{c}_1)\)

The output word is predicted from $\mathbf{s}_1$: \(P(y_1 | \mathbf{s}_1) = \text{softmax}(\mathbf{W}_o \mathbf{s}_1 + \mathbf{b}_o)\)

The model selects the word with highest probability: “I”.

Step 2: Generate “live” (Abbreviated)

2.1 New decoder state: $\mathbf{s}_1 = [0.3, -0.1, 0.5, 0.2]$ (from LSTM update)

2.2 Attention scores:

  • $e_{2,1} = -0.089$ (to “আমি”)
  • $e_{2,2} = 0.156$ (to “ঢাকায়”)
  • $e_{2,3} = 0.592$ (to “থাকি”)

2.3 Attention weights:

  • $\alpha_{2,1} = 0.198$
  • $\alpha_{2,2} = 0.253$
  • $\alpha_{2,3} = 0.549$ (highest attention to “থাকি”)

2.4 Context vector: \(\mathbf{c}_2 = 0.198 \mathbf{h}_1 + 0.253 \mathbf{h}_2 + 0.549 \mathbf{h}_3 = \begin{bmatrix} 0.028 \\ 0.320 \\ 0.633 \\ 0.006 \end{bmatrix}\)

2.5 Output: The model generates “live” with high probability.

Step 3: Generate “in Dhaka”

3.1 Attention focuses on “ঢাকায়”:

  • $\alpha_{3,1} = 0.089$ (to “আমি”)
  • $\alpha_{3,2} = 0.756$ (to “ঢাকায়”)
  • $\alpha_{3,3} = 0.155$ (to “থাকি”)

3.2 Context is dominated by $\mathbf{h}_2$: \(\mathbf{c}_3 \approx 0.756 \mathbf{h}_2 + \text{small contributions}\)

3.3 Output: The model generates “in Dhaka”.

Complete Attention Matrix

The attention weights across all steps form this matrix:

 আমি (I)ঢাকায় (Dhaka)থাকি (live)
I0.3570.2390.405
live0.1980.2530.549
in0.0890.7560.155
Dhaka0.0890.7560.155

Key observations:

  1. Diagonal tendency: The model learns approximate monotonic alignment
  2. Soft alignment: No hard 1-0 decisions; attention is distributed
  3. Context sensitivity: Attention changes based on what’s been generated
  4. Semantic coherence: “live” attends most to “থাকি”, “Dhaka” to “ঢাকায়”

Information Flow Analysis

Gradient flow during training:

  • Loss propagates back through softmax to attention scores
  • Scores receive gradients proportional to attention weights
  • Encoder states receive weighted gradients: $\frac{\partial L}{\partial h_j} = \sum_i \alpha_{ij} \frac{\partial L}{\partial c_i}$

Attention learning dynamics:

  • Initially: attention is nearly uniform (random weights)
  • During training: attention learns to focus on relevant positions
  • Convergence: attention develops interpretable alignment patterns

Bahdanau vs. Luong Attention: Architectural Deep Dive

Real-world performance impact chart comparing translation quality metrics between traditional seq2seq models and attention-enhanced models, demonstrating significant improvements in BLEU scores and translation accuracy

Architectural Differences

Bahdanau (2014) - “Neural Machine Translation by Jointly Learning to Align and Translate”:

Architecture flow:

  1. Previous decoder state: $\mathbf{s}_{i-1}$
  2. Compute attention scores:
    \(e_{ij} = \mathbf{v}_a^T \tanh(\mathbf{W}_a [\mathbf{s}_{i-1}; \mathbf{h}_j] + \mathbf{b}_a)\)
  3. Attention weights: $\alpha_{ij} = \text{softmax}(e_{ij})$
  4. Context vector: \(\mathbf{c}_i = \sum_j \alpha_{ij} \mathbf{h}_j\)
  5. Feed context into RNN:
    \(\mathbf{s}_i = f(\mathbf{s}_{i-1}, y_{i-1}, \mathbf{c}_i)\)
  6. Output prediction:
    \(P(y_i) = g(\mathbf{s}_i, \mathbf{c}_i, y_{i-1})\)

Luong (2015) - “Effective Approaches to Attention-based Neural Machine Translation”:

Architecture flow:

  1. First compute RNN state:
    \(\mathbf{s}_i = f(\mathbf{s}_{i-1}, y_{i-1})\)
  2. Compute attention scores:
    \(e_{ij} = \text{score}(\mathbf{s}_i, \mathbf{h}_j)\)
  3. Attention weights: $\alpha_{ij} = \text{softmax}(e_{ij})$
  4. Context vector: \(\mathbf{c}_i = \sum_j \alpha_{ij} \mathbf{h}_j\)
  5. Combine after RNN:
    \(\tilde{\mathbf{h}}_i = \tanh(\mathbf{W}_c [\mathbf{c}_i; \mathbf{s}_i])\)
  6. Output prediction:
    \(P(y_i) = \text{softmax}(\mathbf{W}_s \tilde{\mathbf{h}}_i)\)

Score Function Comparison

Bahdanau scoring function: \(\text{score}(\mathbf{s}_{i-1}, \mathbf{h}_j) = \mathbf{v}_a^T \tanh(\mathbf{W}_a [\mathbf{s}_{i-1}; \mathbf{h}_j] + \mathbf{b}_a)\)

Computational complexity: $O(d_a \cdot 2d + d_a) = O(d_a d)$ where $d_a$ is attention dimension.

Luong scoring functions:

  1. Dot: $\text{score}(\mathbf{s}_i, \mathbf{h}_j) = \mathbf{s}_i^T \mathbf{h}_j$ — $O(d)$
  2. General: $\text{score}(\mathbf{s}_i, \mathbf{h}_j) = \mathbf{s}_i^T \mathbf{W}_a \mathbf{h}_j$ — $O(d^2)$
  3. Concat: $\text{score}(\mathbf{s}_i, \mathbf{h}_j) = \mathbf{v}_a^T \tanh(\mathbf{W}_a [\mathbf{s}_i; \mathbf{h}_j])$ — $O(d_a d)$

Performance Analysis

Translation Quality (BLEU scores on WMT’14 EN→DE):

  • Bahdanau et al. (2014): ~15.0 BLEU (original paper)
  • Luong et al. (2015): 20.9 BLEU (global attention), 25.9 BLEU (ensemble)

Speed comparison:

  • Bahdanau: Slower due to MLP computation for each position pair
  • Luong (dot): Fastest, pure matrix operations
  • Luong (general): Moderate, one matrix multiply per pair

Memory usage:

  • Bahdanau: Higher due to concatenation and MLP parameters
  • Luong (dot): Minimal, no additional parameters
  • Luong (general): Moderate, single transformation matrix

Mathematical Properties and Theoretical Analysis

Key mathematical properties of attention mechanisms including normalization constraints, probability distribution properties, and computational complexity analysis with detailed mathematical derivations

Softmax Properties

Step-by-step breakdown of the softmax function in attention computation, showing how raw alignment scores are transformed into normalized probability distributions that sum to one

1. Probability Simplex: Attention weights lie on the $(T-1)$-dimensional probability simplex: \(\Delta^{T-1} = \{\boldsymbol{\alpha} \in \mathbb{R}^T : \alpha_j \geq 0, \sum_{j=1}^T \alpha_j = 1\}\)

2. Temperature sensitivity: The softmax temperature controls attention sharpness: \(\alpha_{ij}(\tau) = \frac{\exp(e_{ij}/\tau)}{\sum_k \exp(e_{ik}/\tau)}\)

As $\tau \to 0$: $\alpha_{ij} \to$ one-hot (hard attention) As $\tau \to \infty$: $\alpha_{ij} \to 1/T$ (uniform attention)

3. Gradient magnitude: The gradient of softmax has bounded magnitude: \(\left\|\frac{\partial \alpha_{ij}}{\partial e_{ik}}\right\| \leq \frac{1}{4}\)

This prevents exploding gradients in the attention mechanism.

Context Vector Properties

1. Convex hull: The context vector lies in the convex hull of encoder states: \(\mathbf{c}_i \in \text{conv}\{\mathbf{h}_1, \mathbf{h}_2, \ldots, \mathbf{h}_T\}\)

2. Expectation interpretation: \(\mathbf{c}_i = \mathbb{E}_{j \sim \text{Cat}(\boldsymbol{\alpha}_i)}[\mathbf{h}_j]\)

The context is the expected encoder state under the attention distribution.

Context vector construction diagram illustrating how attention weights are applied to encoder hidden states to create a weighted sum that forms the dynamic context vector for each decoder step

3. Variance bound: The variance of the context vector is bounded: \(\text{Var}[\mathbf{c}_i] \leq \frac{1}{4} \max_{j,k} \|\mathbf{h}_j - \mathbf{h}_k\|^2\)

Maximum variance occurs when attention is uniform.

Information-Theoretic Perspective

Attention as Information Retrieval

Mutual information interpretation: Attention can be viewed as maximizing mutual information between the context and target output: \(I(\mathbf{c}_i; y_i) = H(y_i) - H(y_i | \mathbf{c}_i)\)

The attention mechanism learns to create contexts $\mathbf{c}_i$ that are maximally informative about $y_i$.

Entropy of attention distribution: \(H(\boldsymbol{\alpha}_i) = -\sum_{j=1}^T \alpha_{ij} \log \alpha_{ij}\)

  • High entropy: distributed attention (uncertainty about alignment)
  • Low entropy: focused attention (confident alignment)

KL divergence from uniform: Measures how different attention is from uniform: \(D_{KL}(\boldsymbol{\alpha}_i \| \mathbf{u}) = \sum_{j=1}^T \alpha_{ij} \log \frac{\alpha_{ij}}{1/T} = \log T - H(\boldsymbol{\alpha}_i)\)

Attention Alignment Quality

Alignment error: For supervised alignment data, we can measure: \(\text{AER} = 1 - \frac{2|A \cap S|}{|A| + |S|}\) where $A$ is automatic alignment and $S$ is sure human alignment.

Expected alignment: The expected alignment position is: \(\mathbb{E}[j | \boldsymbol{\alpha}_i] = \sum_{j=1}^T j \cdot \alpha_{ij}\)

Alignment variance: Measures spread of attention: \(\text{Var}[j | \boldsymbol{\alpha}_i] = \sum_{j=1}^T (j - \mathbb{E}[j])^2 \alpha_{ij}\)

Gradient Flow and Training Dynamics

Gradient Computation

Context vector gradient: \(\frac{\partial L}{\partial \mathbf{c}_i} = \frac{\partial L}{\partial \mathbf{s}_i} \frac{\partial \mathbf{s}_i}{\partial \mathbf{c}_i}\)

Attention weight gradient: \(\frac{\partial L}{\partial \alpha_{ij}} = \frac{\partial L}{\partial \mathbf{c}_i} \frac{\partial \mathbf{c}_i}{\partial \alpha_{ij}} = \frac{\partial L}{\partial \mathbf{c}_i} \mathbf{h}_j\)

Encoder state gradient: \(\frac{\partial L}{\partial \mathbf{h}_j} = \sum_{i=1}^S \alpha_{ij} \frac{\partial L}{\partial \mathbf{c}_i} + \sum_{i=1}^S \sum_{k=1}^T \frac{\partial L}{\partial \alpha_{ik}} \frac{\partial \alpha_{ik}}{\partial e_{ik}} \frac{\partial e_{ik}}{\partial \mathbf{h}_j}\)

Training Dynamics Analysis

Attention learning phases:

  1. Random phase (early training): Attention weights are nearly uniform \(\alpha_{ij} \approx \frac{1}{T} + \epsilon_{ij}, \quad |\epsilon_{ij}| \ll \frac{1}{T}\)

  2. Specialization phase: Attention starts to focus on relevant positions \(H(\boldsymbol{\alpha}_i) \text{ decreases over time}\)

  3. Convergence phase: Attention stabilizes to interpretable patterns \(\frac{d}{dt} \boldsymbol{\alpha}_i \to 0\)

Learning rate sensitivity: Attention parameters typically need smaller learning rates: \(\eta_{\text{attention}} = \beta \cdot \eta_{\text{base}}, \quad \beta \in [0.1, 0.5]\)

Attention pattern visualization showing heatmap representation of attention weights across source and target sequences, revealing alignment patterns and focus areas during translation

Gradient Flow Properties

Gradient scaling: The gradient through attention is scaled by attention weights: \(\frac{\partial L}{\partial \mathbf{h}_j} \propto \sum_i \alpha_{ij} \frac{\partial L}{\partial \mathbf{c}_i}\)

Implications:

  • Encoder positions with high attention receive larger gradients
  • Low-attention positions receive smaller gradient updates
  • This creates a feedback loop: relevant positions get more updates

Gradient variance: The variance of gradients through attention: \(\text{Var}\left[\frac{\partial L}{\partial \mathbf{h}_j}\right] = \sum_i \alpha_{ij}^2 \text{Var}\left[\frac{\partial L}{\partial \mathbf{c}_i}\right]\)

Peaked attention (high $\alpha_{ij}^2$) leads to higher gradient variance.

Complete attention process flowchart showing the end-to-end computation from input encoding through attention mechanism to output generation, integrating all components of the attention-based seq2seq model

Real-World Applications

Attention mechanisms have been widely adopted across AI. Notable examples include:

  • Neural Machine Translation: Google’s GNMT (2016) was one of the first large-scale deployments of attention in translation. It used an 8-layer LSTM encoder/decoder with a 1-layer feedforward attention connecting them. Human evaluations showed it reduced translation errors by ~60% compared to the previous phrase-based system. Since then, virtually all state-of-the-art NMT systems use attention or its descendants (e.g. Transformers).

  • Document Summarization: The pointer-generator network by See et al. (2017) augments a seq2seq model with attention and a copy mechanism. It uses attention to decide which parts of the source document to copy into the summary. This model achieved state-of-the-art ROUGE scores on news summarization by allowing the decoder to “point” to source words as needed.

  • Image Captioning: Xu et al. (2015) applied attention to images in the “Show, Attend and Tell” model. A convolutional encoder produces feature vectors for image regions, and an LSTM decoder attends over these regions when generating each word. The model learns to “fix its gaze” on salient parts of the image (like objects) for each word in the caption, significantly improving caption quality on benchmarks.

  • Question Answering (Reading Comprehension): The BiDAF model (Seo et al., 2017) uses bi-directional attention between the question and context passage. At each layer, it computes context-to-question and question-to-context attention, allowing the model to gather query-aware context representations. This approach achieved state-of-the-art results on SQuAD and other QA datasets.

  • Speech Recognition: Chan et al. (2016) introduced “Listen, Attend and Spell” (LAS), an end-to-end ASR model. A listener (pyramidal RNN encoder) processes audio features, and a speller (attention-based decoder) attends to these features to emit characters. In LAS, the decoder is explicitly attention-based: “the speller is an attention-based recurrent network decoder that emits characters as outputs”. This eliminates the need for separate pronunciation models and achieved competitive WER.

These examples illustrate how attention lets models align and extract relevant information from diverse data (text, image, audio) as needed.

Quick Revision Summary

  • Core formulas:

    • Context: $c_i = \displaystyle\sum_{j=1}^T \alpha_{ij}\,h_j$.
    • Weights: $\alpha_{ij} = \exp(e_{ij})\;/\;\sum_{k=1}^T \exp(e_{ik})$.
    • Scores: $e_{ij} = f_{\text{att}}(s_{i-1},h_j)$ (Bahdanau) or $f_{\text{att}}(s_i,h_j)$ (Luong).

  • Key intuitions:

    1. Dynamic context: Instead of a fixed vector, the decoder gets a new context $c_i$ for each output step, focusing on relevant input parts.
    2. Soft alignment: Attention computes a probability distribution $\alpha_{ij}$ over source tokens, effectively “aligning” output words to input words softly.
    3. Weighted sum: The context $c_i$ is a weighted average of encoder states, an expected source representation under the attention weights.
    4. Learned end-to-end: The model learns where to attend by gradient descent, with no hard rules.

  • Bahdanau vs Luong:

    • Decoder state: Bahdanau uses $s_{i-1}$ (prev. state) in scoring; Luong uses $s_i$ (current).
    • Scoring: Bahdanau’s is additive (an MLP with parameters $v_a,W_a$); Luong’s is multiplicative (e.g. dot-product).
    • Use of context: Bahdanau feeds $c_i$ into the RNN update; Luong applies attention after RNN update.
    • Speed: Dot-product (Luong) is typically much faster/cheaper than the additive MLP (Bahdanau).
    • Typical performance: Both improve translation BLEU greatly. Luong’s models (with ensembling) reached ~25.9 BLEU on English–German, slightly above Bahdanau’s original baseline.

  • Attention mechanism steps:

    1. Identify encoder states ${h_j}$ to consider.
    2. Score each $h_j$ against the decoder state $s$.
    3. Normalize via softmax to get $\alpha_{ij}$.
    4. Compute context $c_i = \sum_j \alpha_{ij}h_j$.
    5. Decode the next word $y_i$ using $c_i$ and the RNN.

  • Mathematical insights:

    1. Softmax creates competition: Higher scores suppress others through normalization
    2. Context as expectation: $c_i = \mathbb{E}_{j \sim \alpha_i}[h_j]$ provides statistical interpretation
    3. Gradient flow: Attention weights determine how gradients flow back to encoder
    4. Information theory: Attention maximizes mutual information $I(c_i; y_i)$

  • Training dynamics:

    1. Phase transitions: Random → Specialization → Convergence
    2. Entropy decay: $H(\alpha_i)$ decreases as model learns alignments
    3. Gradient scaling: High-attention positions receive larger gradient updates
    4. Self-stabilization: Converged attention is resistant to further changes

  • Performance gains: In NMT, adding attention gave +5–10 BLEU over non-attentional models. Attentional models also handle long sentences much better – their performance stays high as length increases, whereas non-attention models degrade. (For example, GNMT’s 60%-error reduction was largely thanks to attention.) The main cost is extra computation (roughly 2–3× overhead) but it’s easily parallelizable.

  • Modern extensions: Today’s models build on attention. For example, the Transformer (Vaswani et al., 2017) uses only attention (no RNN/CNN). It introduces self-attention (the model attends to different positions within a single sequence) and multi-head attention (learning multiple ways to attend). These advances have revolutionized NLP (e.g. BERT/GPT).

  • Theoretical guarantees:

    1. Lipschitz continuity: Attention function is stable under input perturbations
    2. Bounded gradients: Softmax prevents exploding gradients ($|\nabla| \leq 1/4$)
    3. Convex combinations: Context vectors lie in convex hull of encoder states
    4. Universal approximation: Attention can approximate any alignment function given sufficient capacity

In short: Attention replaces the single static context vector with dynamic, per-step contexts computed by soft-aligning decoder states to encoder states. This lets the model retrieve the right information exactly when it is needed – just as a human translator would. As one might say: Attention provides a learnable, soft indexing mechanism over the input that greatly enhances sequence modeling.

The mathematical framework shows that attention is not just an engineering trick, but a principled approach to information retrieval and gradient flow control in neural networks. The step-by-step derivations reveal why each design choice (softmax, weighted sums, score functions) serves both computational and theoretical purposes.

Sources: Concepts and formulas above are standard in NMT literature. Empirical results (BLEU, error rates) are from major studies. Mathematical properties are derived from first principles and standard analysis. (All quotations and equations are from the cited papers or follow from the mathematical definitions.)

References

🔑 Foundational Papers on Attention

1. Bahdanau et al. (2014) – Neural Machine Translation by Jointly Learning to Align and Translate → Introduced additive attention, solved fixed-length bottleneck in seq2seq.

2. Luong et al. (2015) – Effective Approaches to Attention-based NMT → Proposed dot/general attention, and global vs. local attention.

3. Vaswani et al. (2017) – Attention is All You Need → Introduced the Transformer, with self-attention and multi-head design.

4. Sutskever et al. (2014) – Sequence to Sequence Learning → Baseline encoder-decoder model with RNNs.

5. Cho et al. (2014) – Learning Phrase Representations with RNN Encoder-Decoder → Introduced GRU, demonstrated early seq2seq without attention.

🖼️ Visual Attention

6. Xu et al. (2015) – Show, Attend and Tell → First visual attention for image captioning.

7. Mnih et al. (2014) – Recurrent Models of Visual Attention → Introduced hard attention with RL.

📖 Reading Comprehension

8. Seo et al. (2017) – BiDAF → Bidirectional attention flow between question and context.

9. Wang et al. (2017) – Gated Self-Matching Networks → Gated attention within passages.

🔁 Pointer & Copy Mechanisms

10. Vinyals et al. (2015) – Pointer Networks → Used attention as a pointer for dynamic output lengths.

11. See et al. (2017) – Pointer-Generator Networks → Combined generation and copying for summarization.

🔊 Speech Recognition

12. Chan et al. (2016) – Listen, Attend and Spell → End-to-end speech recognition with pyramidal encoder and attention.

13. Chorowski et al. (2015) – Attention-based Speech Models → Introduced location-aware attention for audio.

🌍 Large-Scale NMT

14. Wu et al. (2016) – GNMT → Google’s production-scale attention-based NMT system.

🧠 Theoretical Insights

15. Koehn & Knowles (2017) – Six Challenges in NMT → Discussed issues like alignment quality and scalability.

16. Ghader & Monz (2017) – What Does Attention Learn? → Showed attention often captures syntax, not just alignment.

📚 Surveys & Tutorials

📦 Codebases

NLP, Deep Learning
attention-mechanism neural-machine-translation bahdanau-attention luong-attention seq2seq encoder-decoder deep-learning mathematics tutorial
This post is licensed under CC BY 4.0 by the author.